[View the accompanying Significant Digits & Measurements Practice Problems here.]
Why Significant Digits?
Significant digits (also called significant figures or “sig figs” for short) indicate the precision of a measurement. A number with more significant digits is more precise. For example, 8.00 cm is more precise than 8.0 cm.
Recording Measurements
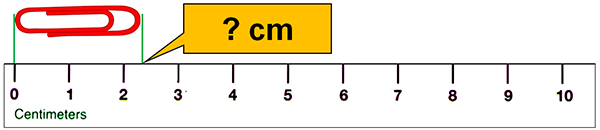
When recording a measurement we include all of the known digits plus a final estimated digit. It’s sometimes easier to think of this in terms of recording all of the known “places” (ones, tenths, hundredths) plus a final estimated place. For example, in the first ruler below it is marked every one centimeter so we know the ones place and could record 2. But we must also estimate one, and only one, additional digit. So in this case we might record 2.3 cm or perhaps 2.4 cm. Either would be correct as the 2 (ones place) is precisely known while the final digit (tenths place) is estimated.
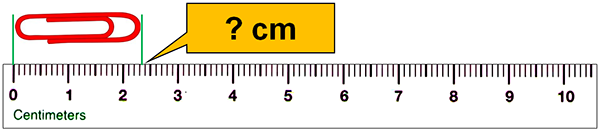
Now consider the next ruler. In this case, the ruler is marked in both ones and tenths meaning that we can clearly see the first part of the measurement is 2.3. However, we must again estimate one additional digit or place – 2.35 cm.
Counting Significant Digits
If a measurement has already been made and provided, then we can determine how many significant digits are present by following a few simple rules.
1. All non-zero numbers are significant.
For example, the number 843 would have three significant digits are they are all non-zero.
2. Zeros between non-zero numbers are significant.
The number 307 would also have three significant digits as the zero is sandwiched between the non-zero numbers 3 and 7.
3. Leading zeros before a number are not significant.
In the number 0.0025, the leading zeros (those to the left of the non-zero numbers) are not significant. Therefore, only the 2 & 5 are counted meaning it has two significant digits. The leading zeros are known as placeholder zeros as they do not add to the precision of the measurement, they simply occupy the ones, tenths, and hundredths places. This will become more clear in our lesson on Scientific Notation as 0.0025 could also be written as 2.5×10-3, completely eliminating the leading zeros.
4. Trailing zeros after a number are not significant unless there’s a decimal point.
Consider three different measurements: 250 versus 250. versus 250.0
250 – The trailing zeros (those to the right of the non-zero numbers) are also placeholders and thus do not add to the precision of the measurement. Thus, there are only two significant digits from the 2 & 5. Again, as we’ll see in our lesson on Scientific Notation, this could be written 2.5×102 completely eliminating the final placeholder zero.
250. – The decimal point indicates the measurement is precisely 250. not around 250 as in the previous example. This number would have three significant digits.
250.0 – Again, the decimal point indicates that the trailing zeros are significant and should be counted meaning there are four significant digits.
Counting Significant Digits Examples
1. 23.5 – Three significant digits as all are non-zero numbers (see rule #1 above).
2. 23.50 – Four significant digits. The final zero is significant because the number contains a decimal place (see rule #4 above).
3. 402 – Three significant digits. The zero is between non-zero numbers (see rule #2 above).
4. 5,200 – Two significant digits. There is no decimal place so the trailing zeros are simply placeholders and not-significant (see rule #4 above).
5. 0.030 – Two significant digits. Leading zeros are never significant (see rule #3 above). The trailing zero is significant because the number contains a decimal place (see rule #4 above).
6. 0.0070080 – Five significant digits. Leading zeros are never significant (see rule #3 above). The two zeros between 7 and 8 are significant because they are between non-zero numbers (see rule #2 above). The trailing zero is significant because the number contains a decimal place (see rule #4 above).
For additional practice problems on significant digits and measurements, visit Significant Digits & Measurements Practice Problems.